一元回归分析在工程检测中的应用

统计学上采用回归分析方法研究成因果关系的相关变量之间的关系。表示原因的变量称为自变量，表示结果的变量称为依变量。即一个自变量与一个依变量的回归分析称为一元回归分析。

一元回归分析又分为线性回归分析与曲线回归分析两种。

在建立一元线性回归方程中，虽然有很多种不同的方法来求样本回归函数，但是在回归分析中最常用的方法就是最小二乘法。

一、最小二乘法的定义

最小二乘法的定义是一种数学优化技术，它通过最小化误差的平方和来寻找数据的最佳函数匹配。最小二乘法通过最小化误差的平方和来求解最优解。这种方法在解决线性方程组、数据拟合等问题时非常有效。

二、最小二乘法在一元回归分析中的应用

如果变量x与y有精确的线性关系比如说 y=bx+a，那么观测值与回归值是相等的。然而在实际工作中诸多变量的关系不一定都是如此，由于受到许多随机因素的干扰使得物与物之间没有那么明确的一一对应关系。那么我们就需要通过数学的方法来使之对应。首先通过试验取得数据，其次把数据绘出来，然后拟合一条跟已知的函数图像最为接近的曲线，这样就可以相对地将他们之间的关系表示出来了，在处理诸如此类的事件中常常应用到最小二乘法。

（一）最小二乘法在线性回归分析中的应用计算

（二）最小二乘法在曲线回归分析中的应用计算

三、一元回归分析在工程检测中的应用

例1：胶水比与实测抗压强度线性方程

根据《普通混凝土配合比设计规程》JGJ 55-2011第6.2.1条第1点根据混凝土试验结果，宜绘制强度和胶水比的线性关系图确定略大于配制强度对应的胶水比。

根据试验数据求线性方程y=bx+a

由数据求得

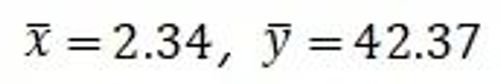
根据上文计算公式

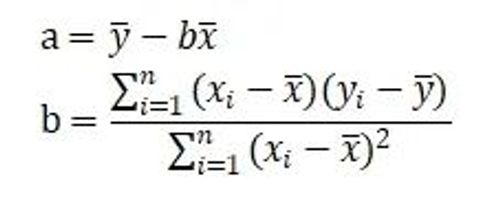
即线性方程y=28.943x-25.457

再利用Excel绘制线性曲线方程，两个方程相同。(如下图1所示)

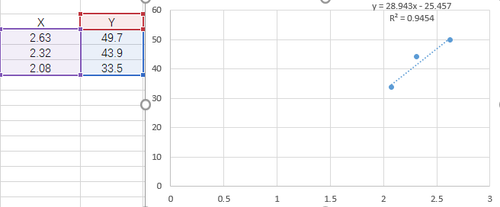
图1 Excel绘制线性方程

例2：土工击实试验ρd-ω关系曲线计算

根据《公路工程无机结合料稳定材料试验规程》JTG3441-2024 T 0809-1994“无机结合料稳定材料击实试验方法”第5.3.2条要求，试验各点宜采用二次曲线方法拟合。

再利用Excel绘制二次曲线方程，两个方程相同。(如下图2所示)

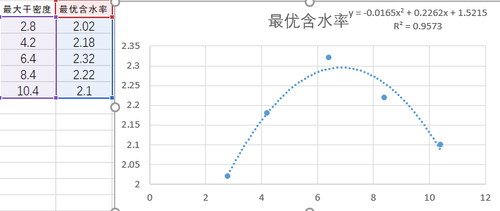
图2 Excel绘制二次曲线方程

一元回归分析在工程检测中的应用还有很多，例如水泥或石灰稳定材料中水泥或石灰剂量测定方法(EDTA滴定法)EDTA二钠标准溶液含量与水泥/石灰剂量标准曲线、平板荷载中千斤顶液压表与荷载强度标准曲线等等。

对于上述击实试验实例中，此次计算是按规范要求采用二次曲线拟合，根据实测数据，还可以进行三次曲线拟合或更高次曲线拟合，拟合出的曲线方程计算出的最优含水率、最大干密度可能更贴合实际数据。有兴趣的小伙伴可以利用上述计算公式或其他软件进行计算研究。

上一篇：亚克力声屏障有哪些优势？其质量...

下一篇：蒸压加气混凝土砌块见证取样试验...