软土地层的易挤性以及施工过程中的偏心加载等均可导致部分工程桩出现倾斜现象,致使桩的承载能力大大降低,严重危害建筑工程质量。目前,建筑桩基技术规范对基桩施工过程中的垂直度检验做了相应的规定,施工完成后基桩垂直度的检验尚未提及。现阶段可采用钻芯法对基桩垂直度进行粗略的估算,由于该方法的局限性,规范未作强制性要求。因此,为确保工程质量,在现有检测手段的基础上,研究一种有效快捷的桩身垂直度测试方法,成为现在基桩检测中亟待解决的一个问题。
目前关于基桩倾斜测试尚处于起步阶段,既没有成熟的分析理论,也没有丰富的工程经验。国内仅广东工程勘察院做了一些模型桩对桩身垂直度测试进行研究,但其测试方向尚缺乏理论依据。本文基于应力波传播理论,将倾斜基桩应力波分解为纵波和弯曲波,运用有限元分析软件进行数值模拟,研究桩身不同点首峰脉冲宽度与倾斜方向和倾斜角度的关系,为基桩垂直度的检测提出了一种新途径。
倾斜基桩应力波分解
将桩身视为一材质均匀、截面恒定的弹性杆。定义倾斜基桩的倾角为θ,假设在倾斜基桩桩顶作用一垂直竖向力F,则力F按倾斜基桩轴线方向可分解为一平行轴线方向的作用力F1和一垂直轴线方向的作用力F2(如图1所示)。
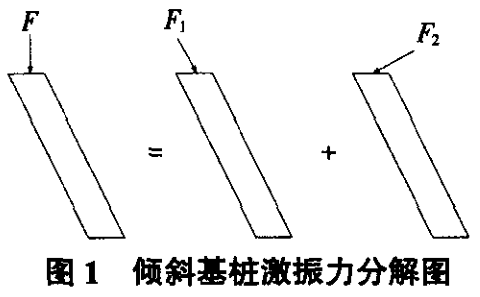
定义在F,F1,F2作用下桩身所产生的的位移分别为u,u1,u2,则u1为桩体中一维纵波的解,u2为桩体中一维弯曲波的解。
将桩体作为研究对象,在桩顶施加一作用力Fi,则倾斜基桩的桩身位移ui可用如下方程进行求解:
控制方程:
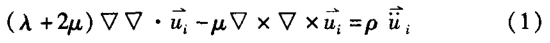
边界条件:
桩周土阻力:
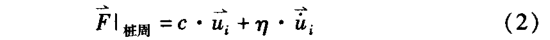
桩底土阻力:
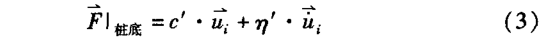
桩顶作用力:

初始条件:
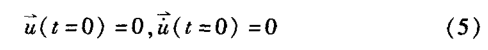
桩顶作用力Fi分别取为F,F1,F2时,桩身位移对应为u,u1,u2。在适定边界条件下,桩身位移u的解具有唯一性,则u=u1+u2。
根据以上推导可知,在把桩体视为一维均质连续弹性杆件的假定下,应力波在倾斜基桩中的传播可分解为一维纵波在桩身中的传播和一维弯曲波在桩身中的传播。
倾斜基桩桩顶各点纵波和弯曲波速度时域信号分析
基桩动测问题的理论基础一维应力波理论只有在锤径桩径比、波长桩径比、桩长桩径比足够大时才能近似成立,否则该问题实际上为应力波在柱体中传播的三维问题,倾斜基桩亦无例外。本节将借助新型有限元分析系统COMSOL Multiphysics对倾斜基桩的动测过程进行三维动态仿真,对桩顶不同接收点应力波波形进行分析,探讨应力波在倾斜基桩中的传播规律。
桩长L=10m,桩径为D=500mm,桩身密度P=2450kg/m3,泊松比v=0.18,弹性模量Ep=3.0×104MPa,桩端固定,桩顶和桩周自由,激振力f=1300000×[1-cos(1000×π×t)]N/m2(0≤t≤2ms),基桩倾斜方向如图2a)所示,桩顶敲击点和信号接收点如图2b)所示。
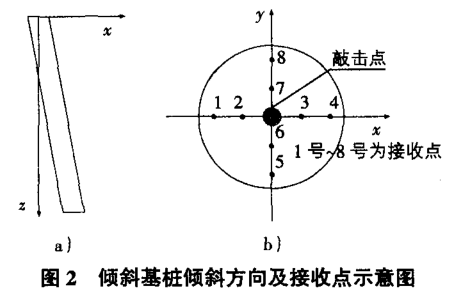
为了探讨倾斜基桩桩顶质点振动速度特征,此处将各桩顶作用力下z方向速度在x-z平面内分解为一沿着轴心方向的速度和一垂直轴心方向的速度(y方向速度可以忽略) ,其分解图形如图3所示(图3b)直桩上所作用竖直向力和水平向力分别与图3a)倾斜基桩上沿着轴向力和垂直轴向力相等)。则倾斜基桩桩顶z方向质点振动速度可分解为v=v1+v2+v3+v4。
以倾角θ为10°的倾斜基桩为例,选取同长度的竖直桩进行比对,桩顶1号,4号,5号,8号接收点的速度时域信号如图4所示。

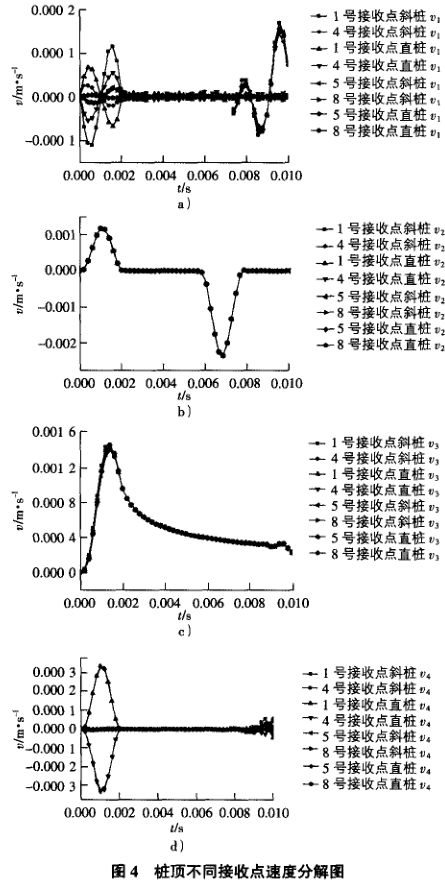
研究首脉冲峰值时间点(1.1ms)的各分速度,从图4中可以看出:
1)速度v1在首脉冲速度峰值时间点时可以忽略不计。
2)在同等条件下,倾斜基桩和竖直桩中速度v2和v3的波形信号完全一致。
3)v4与接收点位置x向坐标成正比,符合材料力学中“当构件受弯曲作用时,其应力大小与所求应力点到中性轴的距离成正比,符合材料力学中“当构件受弯曲作用时,其应力大小与所求应力点到中性轴的距离成正比”的相关原理。分别选取1号一4号接收点和5号一8号接收点测试各分速度信号可知:在首脉冲区间,沿着基桩倾斜方向首脉冲峰值递减,垂直于基桩倾斜方向首脉冲峰值不变。
基桩垂直度的确定
倾斜基桩在采用低应变法检测时,桩顶各点振动速度时域曲线不尽相同,主要区别位于首脉冲区间段。在垂直倾斜方向的轴线上,不同接收点首脉冲区间段的质点振动速度时域曲线基本一致;在沿着基桩倾斜方向上,不同接收点首脉冲区间段的质点振动速度时域曲线变化比较明显,首峰峰值沿基桩倾斜方向有规律的逐渐减小 。本文对基桩桩顶不同接收点的首峰峰值的变化进行数值仿真计算,分析基桩的倾斜方向和倾斜角度。
1确定基桩倾斜方向
建立以倾斜角度为10°的基桩模型,敲击点和接收点位置如图5所示 。
将图5所示各接收点的桩顶质点速度时域曲线进行提取分析其首波峰值,如表1所示。

从表1可以看出,沿基桩倾斜方向(即相同Y坐标时),各信号接收点首波峰值呈线性变化,而在垂直基桩倾斜方向(即相同X坐标时),各信号接收点首波峰值基本不变。
根据上述论断,在桩顶任取三个不在同一直线上的信号接收点进行数据分析,假定三点位置分别为P1,P2,P3(如图6所示),其对应各点信号的首波峰值为a1,a2,a3根据线性插值,求得P1和P3点之间峰值等于a2的点P4,连接P2和P4两点,则通过P2和P4两点的直线为等值线,而垂直该等值线的方向就是基桩倾斜的方向。

2确定基桩倾斜角度
建立倾斜角度分别为 0°,5°,8°,10°,20°的基桩模型,对不同倾斜角度基桩桩顶各点速度时域信号进行提取分析,主要研究其首脉冲峰值。
由第2节中的分析可知,分速度v1可以忽略不计,v2和,v3的波形信号完全一致,v4与接收点位置x向坐标成正比。在此对同一倾斜基桩中各接收点的首脉冲峰值进行直线拟合,定义方程为y=b(x+c),则 b×c可以看作v2和v3的合速度分量 ,b×x则为v4所表示的速度分量。各倾斜角度下基桩桩顶各点首脉冲峰值参数如表2所示。
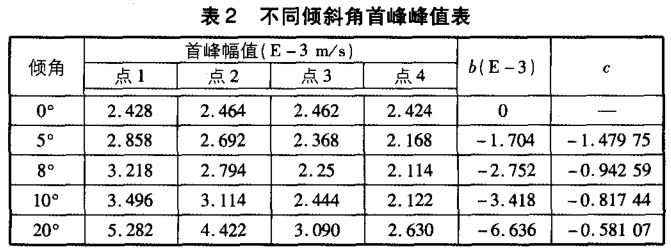
1)计算斜率b。
当倾斜基桩的倾斜角度为θ时,与轴心方向垂直的力的分量大小为桩顶力分量大小的sinθ倍,与轴心方向平行的质点速度在方向的速度分量大小为该质点速度大小的sinθ·cosθ倍。通过数值仿真计算,求得竖直桩水平敲击桩顶不同点竖向质点振动速度大小为v-0.2=0.00392,v0.2=-0.00390,其直线拟合的斜率为-0.0196,则:
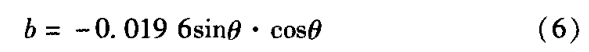
不同倾斜角度情况下斜率b值对比如表3所示。
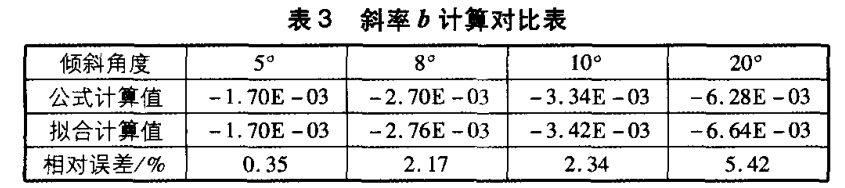
根据表3可知,由公式b=-0.0196sinθ·cosθ计算桩顶不同点的峰值斜率较真实值要小,这是由于忽略v1的影响的缘故,故为了减少相对误差,可对该公式修正为:
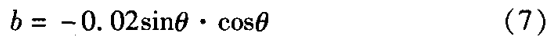
2)计算截距c。
由图3可知v2和v3为不变量,则b×c为速度v2和v3的合速度在z方向的分量,其中力F·cosθ相对应的纵波首脉冲峰值为v2,力F·sinθ相对应的弯曲波首脉冲峰值为v3。
定义Vz为力F的纵波速度信号幅值,Vw为力F的弯曲波速度信号幅值,则:

根据本文中所采用的计算模型计算得Vz=0.00244,Vw=0.01494。根据式(7),式(8)可得:

若截距C已知,则可用式(9)求得其倾斜角度θ,计算公式如下所示:
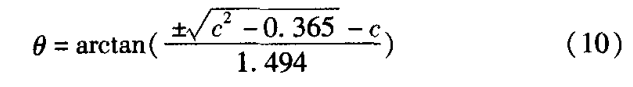
鉴于工程实际情况,基桩的倾斜角度在施工过程中不会太大,故计算时我们取其小值。式(10)仅当C<-0.604时有解,由表2的截距和共同计算的倾斜角度的相对误差如表4所示。

3)不同影响因子下的斜率b和截距c。
不同力、脉宽、桩长、桩径条件下计算的斜率b和截距c 如表5所示,其中点1坐标为(-0.3,0),点2坐标为(-0.15,0),点3坐标为(0.15,0),点4坐标为(0.3,0)。从表5可以看出,斜率与脉冲宽度和桩长的相关性不大,斜率与力的大小成正比,斜率反比于桩径的三次幂。
截距与桩顶作用力大小、脉冲宽度、桩长对截距的相关性不是很大,因斜率与桩径的三次幂成反比关系,而b×c与桩径的平方成反比,则截距与桩径成正比。
对式(10)考虑桩径修正以后为:
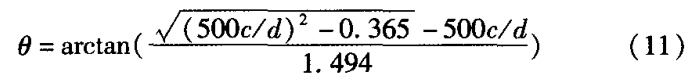
4)考虑土阻力的影响。
不同土阻力对截距的影响如表6所示。

从表6可得,截距c随着土阻力的增加而减小,但影响较小。考虑到本文中倾斜角度的计算主要是指基桩浅部的倾斜情况,故实际检测过程中可以忽略土阻力的影响。
实例分析
该工程模型桩由广东工程勘察院提供:桩顶用尼龙锤头竖向同点进行激震,采用加速度计拾震。测点号如图7所示(接收点距离圆心150mm),该桩桩长7m,桩径500mm,倾斜角度8°,倾斜方向为由北向南倾斜。

测试得到顶各点z方向质点振动速度实测曲线,如图8所示。
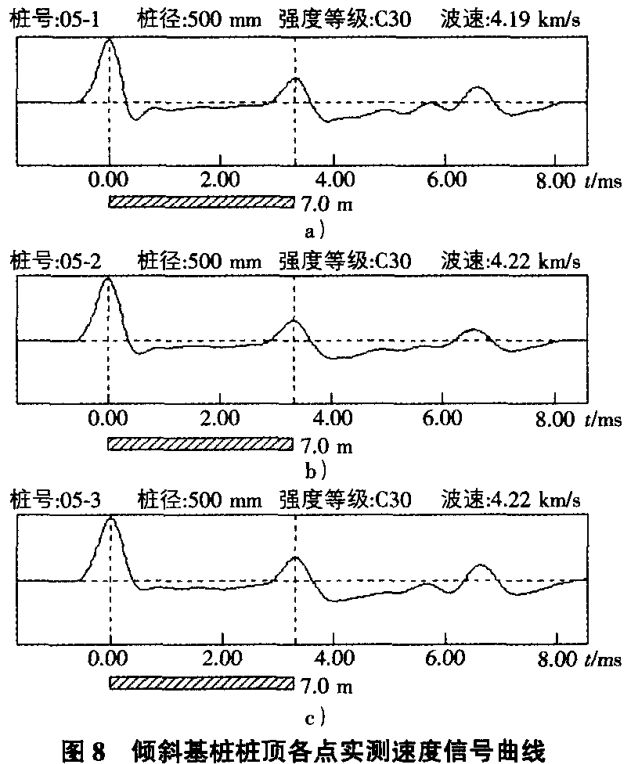
此处用桩顶首波峰值与桩底反射波峰值的比值替代原公式中的桩顶首波峰值。列3接收点首峰峰值如表7所示。
采用上述倾斜方向测试方向可知倾斜方向为北偏东4.6°,由北向南倾斜,对任意两点(1号,2号接收点)沿倾斜方向作直线拟合有截距c=1.002,代入倾斜角度计算公式(11)可计算得出倾角θ=7.74°,与实际倾角误差为3.3%。由上可知倾斜方向和倾斜角度模型桩数据误差很小,满足工程实际要求。
结语
倾斜基桩在桩顶部不同点拾震时有许多有规律的变化,本文分析表明:
1)一维情况下,倾斜基桩桩身应力波可分解为同长度的纵波和弯曲波叠加。
2)在桩顶中心敲击,沿着倾斜方向接收时,桩顶接收信号首峰峰值线性减小,而垂直倾斜方向接收,桩顶接收信号不变。
3)在倾斜基桩桩顶选取任意不在同一直线上的三点进行信号拾取,可运用文中所属方法初步估算基桩倾斜方向和倾斜角度。
4)基桩倾斜角度沿桩身不断变化的情况需进一步研究。
下一篇:贯入式混凝土强度检测仪操作方法