业内普遍认为造成残余应力的原因主要有三种:温度差异、金属相变、机械加工。
网络上对残余应力的描述林林总总。今天小编从机械加工的角度,基于加工过程和构件受力演示一遍残余应力的计算,让大家更直观地感受残余应力的存在。
一、从机械加工理解残余应力
机械加工,是一种改变金属材料性能和外形的手段。采用热轧、冷弯、挤压、冷拉、冷镦等工艺将原材料加工成所需要的金属件的过程,本质上仍然是通过力加载或位移加载的方式对原材料施加外荷载,从而达到改变原材料机械性能和外形的目的。
工程领域的人都知道,评估金属机械性能一般通过拉伸三项试验(屈服强度、抗拉强度、断后延伸率)甚至拉伸四项(多了一项断面收缩率)。
以检测钢板原材料屈服强度为例,一般会从钢板上随机裁切一段做拉伸试验,检测出来的屈服强度就被认为是该钢板的屈服强度。
不过,如果在该钢板选取5个部位检测屈服强度,那么5个部位的屈服强度极大概率是或大或小,而非完全一样。
说到这里,我们会意识到,即使采用同一种工艺加工出来的产品(甚至同一个金属产品),我们最多认为该产品各部位机械性能基本稳定,但是不能说各部位机械性能一样,这个认知对于理解残余应力来说非常重要!
上面提到的钢板,会被运到加工厂继续加工。
以加工压型钢板为例,裁切好的钢板会被放置到模具台上向轧辊输送,通过轧辊将原本平坦的钢板“弯折”成压型钢板模样。
很关键的一点是,对于加工精度较高的压型钢板,往往需要多个轧辊。这是因为钢板经过一道轧辊成型之后部分区域会有回弹现象,不足以使被弯折的钢板有足够的平整度,根本原因在于前面说到的钢板自身各个区域的强度有大有小。
我们假设Q235B钢板三块连续区域的实际屈服分别是240MPa、250MPa、280MPa,轧辊造成钢板变形时产生的应力是250MPa,经过一道成型工艺之后,屈服是240MPa的区域会产生较大永久变形,250MPa的区域会产生微量永久变形,屈服是280MPa的区域则在短暂的变形之后完全回弹,三部分变形程度不一样导致它们之间相互拉扯产生约束形成超静定结构,它们之间的这种应力就是所谓的“残余应力”——轧辊过后,外部作用消除,内部依然有应力、有约束。
二、残余应力计算
残余应力的计算非常复杂,工程上多用结构仿真软件模拟计算。
下面我们将上述钢板简化成图1金属构件计算残余应力,从数据上感受残余应力的存在。需要说明的是,本案例仅用于理解残余应力,不代表真实的产品设计。
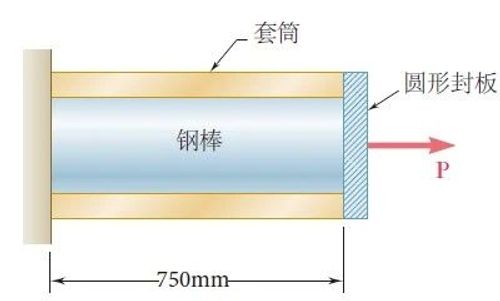
图1构件
图1构件的左侧被固定,右侧通过圆形封板对其施加外力P,构件的外围是屈服强度σt,y=300MPa、弹性模量Et=100GPa的套筒,截面积为65mm2;内部是屈服强度σr,y=250MPa、弹性模量Er=200GPa的钢棒,截面积为50mm2。构件的两部分都是理想的弹塑性材料(需要特别说明的是,我们在这里对构件内、外区域的材质赋予不同力学参数是为了模拟同一个产品不同部位的机械性能)。当P从0kN增加至25kN,再卸载至0kN之后,计算套筒和钢棒中各自的残余应力。
根据构件信息:
钢棒的最大承载力是
Pr=250×50=12.5kN
对应的最大应变是
εr=σr,y/Er=250/200/103=0.00125
对应的最大伸长量是
δr=L×εr=750×0.00125=0.9375mm
力-位移曲线如图2所示:
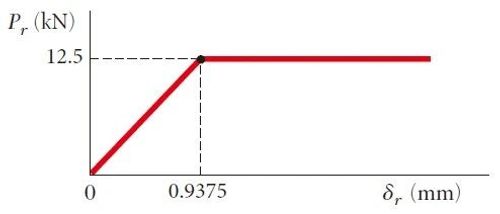
图2钢棒力-位移曲线
套筒的最大承载力是
Pt=300×65=19.5kN
对应的最大应变是
εt=σt,y/Et=300/100/103=0.003
对应的最大伸长量是
δt=L×εt=750×0.003=2.25mm
力-位移曲线如图3所示:

图3套筒力-位移曲线
为了观察两部分作为一个整体构件在荷载作用下的表现,我们把图2和图3合并成图4(合并过程兹不赘述):
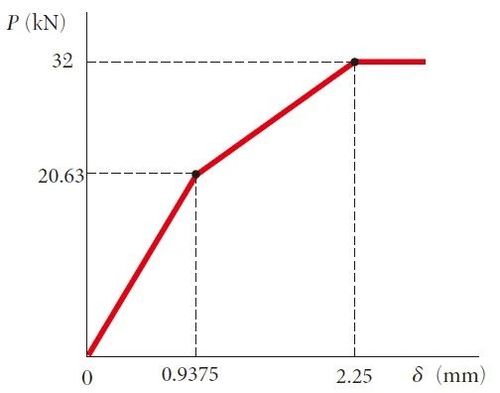
图4构件作为整体力-位移曲线
从0kN加载至25kN
正如图3表示的那样,钢棒最大承载力为12.5kN,此后随着位移增加承载力不再提高,那么当P加载至25kN时,套筒分担的荷载是
P't=25-12.5=12.5kN
对应地,套筒应力
σ't=P't/At=12500/65=192.3MPa
对应地,套筒的伸长量
δt=L×ε't=750×192.3/100/103=1.44mm
也就是说在25kN作用下,整个构件能达到的最大伸长量为
δmax=δt=1.44mm
将P从25kN卸载至0kN
对于弹塑性钢材,弹性模量是恒定的,因此卸载过程中,构件的力-位移关系会遵从图5中的CE路径。当P=0kN时,CE与横轴的交点就是构件的永久变形δp。CE斜率(也就是构件整体弹性模量)等于图4中的第一段曲线斜率,那么EF段——即构件整体回弹量δ'为
δ'=-25×(0.9375/20.63)=-1.14mm
那么永久变形
δp=δmax+δ'=1.44-1.14=0.3mm

图5 卸载之后的永久变形
到这里写了这么多,梳理成一句话就是:给图1构件从0kN开始施加荷载至25kN,内部钢棒已经进入塑性阶段,而外部套筒仍然处于弹性工作阶段;再卸载至0kN,外荷载消失,内部钢棒恢复一部分变形之后产生永久变形,外部套筒虽然有能力完全恢复变形,但是由于套筒和钢棒做为一个整体,因此套筒恢复变形的趋势被钢棒所牵制,该构件内部(也就是套筒和钢棒之间存在“牵扯”,钢棒受压、套筒受拉)存在约束形成超静定结构,这种约束力即所谓的“残余应力”。
三、接下来,如何求解残余应力?
残余应力,“残余”的意思就是加载产生的应力减去卸载之后构件恢复那部分变形所对应的应力,这部分残余应力对应构件的永久变形。
根据上面得到的永久变形可以计算对应的应变
ε''=-1.14/750=0.00152
构件各部分的应变相同,各部分的应力为
套筒:σ''t=ε''×Et=-152MPa
钢棒:σ''r=ε''×Er=-304MPa
构件各部分残余应力
套筒:
σt,res=σ't+σ''t=192.3-152MPa=40.3MPa
钢棒:
σr,res=σr+σ''r=250-304MPa=-54MPa
其中,192.3MPa和250MPa分别对应P=25kN时套筒和钢棒的内应力。